【专题】Dijkstra

发表于 分类于 ， 本文字数： 1.3k 阅读时长 ≈ 2 分钟
图论专题，介绍Dijkstra算法

简介

Dijkstra算法是求解单源最短路的算法之一，核心思想是贪心，只适用于边权为正的无向和有向图。原复杂度\(O(n^{2})\)，优化后时间复杂度能到\(O(mlog_{m})\)。

Dijkstra算法

首先我们来看这个贪心性质：

从起点u到终点v的最短路径，一定是从起点u到这条最短路径上经过的点w的最短路径。

可以用反证法证明，假设\(dis(u, w)\)是起点u到终点v最短路径上的起点u到途经点w的距离。若存在不是最短路径上的\(dis'(u, w) < dis(u, w)\)，那么可以得出\(dis'(u, w)+dis(w, v) < dis(u, w)+dis(w, v)\)，即存在从起点u到终点v的更短的路径，与假设矛盾。

可以根据这个性质得到贪心思路，但是这个性质基于一个前提：

对于起点u的最短邻接边uw，从u到w不可能存在比\(dis(u, w)\)更短的路径。因为uw已经是最短的了，从其它路径走的话必然经过比uw更长的路径。

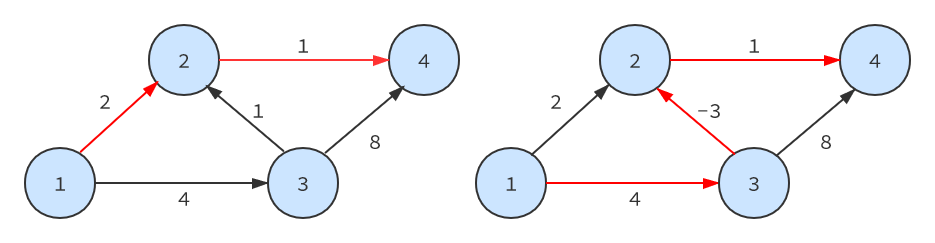
而这也是Dijkstra不能处理负边权的原因，如果有负边权则无法满足前提。可以看下图自行理解：

那么，依据这个贪心性质得到思路，我们可以从现知的最短路径开始，去更新起点到其它点的距离，再更新已知的最短路，重复这个过程，遍历完所有的点之后，就能得到起点到其它点的最短路径长度。详细过程如下：

  1. 将起点加入已经确定最短路的集合S，其它点则属于未确定的集合V-S=T。
  2. 更新到起点的最短距离dis[i]。
  3. 选取未访问的最小的dis[x]，标记并加入已经确定最短路的集合S，此时的dis[x]就是x到起点的最短距离。
  4. 再依据$ dis[y]=min(dis[y], dis[x]+{边权值}w[x][y]) \(，更新集合T中与x相邻的点y到起点的最短距离dis[y]。这个操作叫做`松弛操作（relax）`，更新过后当前的不等式约束\) dis[y] \(相对于\) dis+w[x][y] $已经不是最“紧”的约束了，下一次更新dis[y]时就不需要检查这个约束了，即原约束被“松弛”了。
  5. 重复3，4步骤直到目标点加入集合，此时目标点对应的dis[v]就是最短路径长度。

邻接矩阵存图，核心代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void dijkstra(int s, int n)
{
    dis[s] = 0;
    for(int i=1; i<=n; i++)
    {
        int x = 0;
        for(int j=1; j<=n; j++)
            if(!vis[j] && (x==0 || dis[j]<dis[x])) x = j;

        vis[x] = 1;
        for(int j=1; j<=n; j++)
            dis[j] = min(dis[j], dis[x]+g[x][j]);
    }
}

优化

时间复杂度分析，只分析集合操作，n次delete-min，m次decrease-key。

  • 如果用暴力：\(O(n^{2}+m)\)。
  • 如果用堆：\(O(mlog_{n})\)。
  • 如果用priority_queue：\(O(mlog_{m})\)。
  • 如果用线段树（ZKW线段树）：\(O(mlog_{n}+n)=O(mlog_{n})\)。
  • 如果用Fibonacci堆：\(O(nlog_{n}+m)\)。

如果使用priority_queue，无法删除某一个旧的结点，只能插入一个权值更小的相同编号结点，这样操作导致堆中元素是\(O(m)\)的。

下面给出使用邻接表及priority_queue的优化版本，即优化了存图方式以及寻找未访问的最小dis结点过程。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void dijkstra(int s, int n)
{
    q.push({dis[s]=0, s});
    while(!q.empty()){
        int u = q.top().second; q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i=H[u]; ~i; i=e[i].next){
            int v=e[i].to, w=e[i].w;
            if(!vis[v] && dis[u]+w < dis[v]){
                dis[v] = dis[u]+w;
                pre[v] = u;
                q.push({dis[v], v});
            }
        }
    }
}
展开代码
收起代码

模板

原始版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
const int inf = 0x3f3f3f3f;
const int mxn = 1e3 + 5;

int g[mxn][mxn];

void graph_init(int n)
{
    for(int i=1; i<=n; i++){
        for(int j=1; j<=n; j++)
            g[i][j] = inf;
        g[i][i] = 0;
    }
}

int dis[mxn], pre[mxn];
bool vis[mxn];

void dijkstra_init(int n)
{
    for(int i=1; i<=n; i++){
        vis[i] = pre[i] = 0;
        dis[i] = inf;
    }
}

void dijkstra(int s, int n)
{
    dis[s] = 0;
    for(int i=1; i<=n; i++)
    {
        int x = 0;
        for(int j=1; j<=n; j++)
            if(!vis[j] && (x==0 || dis[j]<dis[x])) x = j;

        vis[x] = 1;
        for(int j=1; j<=n; j++){
            if(!vis[j] && dis[x]+g[x][j] < dis[j]){
                dis[j] = dis[x]+g[x][j];
                pre[j] = x;
            }
        }
    }
}

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    graph_init(n);

    for(int i=0; i<m; i++)
    {
        int u, v, w;
        scanf("%d %d %d", &u, &v, &w);
        g[u][v] = w;
    }
    dijkstra_init(n);
    dijkstra(1, n);

    for(int i=1; i<=n; i++)
        printf("%d ", dis[i]);
    printf("\n");

    for(int i=n; i; i=pre[i])
        printf("%d ", i);
    printf("\n");

    return 0;
}

/*
Sample Input:

4 5
1 2 2
1 3 4
2 4 1
3 2 1
3 4 8

Sample Output:

0 2 4 3
4 2 1

*/
展开代码
收起代码

优化版本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
const int inf = 0x3f3f3f3f;
const int mxn = 1e3 + 5;

struct E {
    int to, next, w;
} e[mxn];

int H[mxn], tot;

void add(int from, int to, int w) {
    e[tot] = {to, H[from], w};
    H[from] = tot++;
}

void graph_init(int n)
{
    for(int i=1; i<=n; i++)
        H[i] = -1;
    tot = 0;
}

int dis[mxn], pre[mxn];
bool vis[mxn];
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;

void dijkstra_init(int n)
{
    for(int i=1; i<=n; i++){
        vis[i] = pre[i] = 0;
        dis[i] = inf;
    }
}

void dijkstra(int s, int n)
{
    q.push({dis[s]=0, s});
    while(!q.empty()){
        int u = q.top().second; q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i=H[u]; ~i; i=e[i].next){
            int v=e[i].to, w=e[i].w;
            if(!vis[v] && dis[u]+w < dis[v]){
                dis[v] = dis[u]+w;
                pre[v] = u;
                q.push({dis[v], v});
            }
        }
    }
}

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    graph_init(n);

    for(int i=0; i<m; i++)
    {
        int u, v, w;
        scanf("%d %d %d", &u, &v, &w);
        add(u, v, w);
    }
    dijkstra_init(n);
    dijkstra(1, n);

    for(int i=1; i<=n; i++)
        printf("%d ", dis[i]);
    printf("\n");

    for(int i=n; i; i=pre[i])
        printf("%d ", i);
    printf("\n");

    return 0;
}

/*
Sample Input:

4 5
1 2 2
1 3 4
2 4 1
3 2 1
3 4 8

Sample Output:

0 2 4 3
4 2 1

*/
展开代码
收起代码